SoSpin, a C++ library for Yukawa decomposition in SO(2N) models

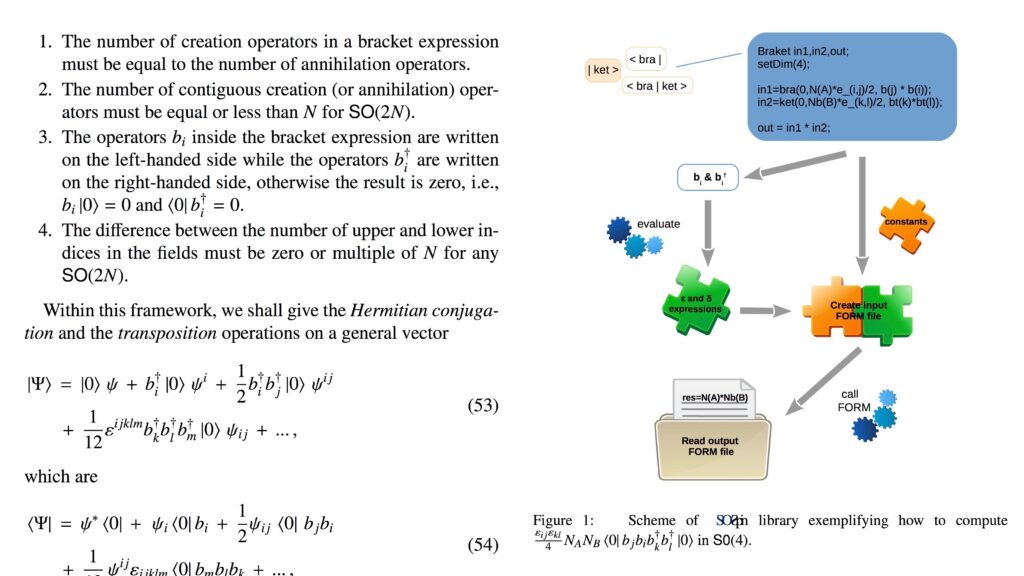
We present in this paper the SoSpin in library, which calculates an analytic decomposition of the Yukawa interactions invariant under SO(2N) in terms of an SU(N) basis. We make use of the oscillator expansion formalism, where the SO(2N) spinor representations are expressed in terms of creation and annihilation operators of a Grassmann algebra acting on a vacuum state. These noncommu- tative operators and their products are simulated in SO pS in through the implementation of doubly-linked-list data structures. These data structures were determinant to achieve a higher performance in the simplification of large products of creation and annihilation operators. We illustrate the use of our library with complete examples of how to decompose Yukawa terms invariant under SO(2N) in terms of SU(N) degrees of freedom for N = 2 and 5. We further demonstrate, with an example for SO(4), that higher dimensional field-operator terms can also be processed with our library. Finally, we describe the functions available in SoSpin in that are made to simplify the writing of spinors and their interactions specifically for SO(10) models.